Question

An airplane travels 3675 kilometers against the wind in 5 hours and 4275 kilometers with the wind in the same amount of time. What is the rate of the plane in still air and what is the rate of the wind?

Answer 1

Plane: 795km/h

Wind: 60km/h

Explanation:

We have that the speed is given as follows:

`\begin{gathered} v=(d)/(t) \\ \\ d=vt \end{gathered}`

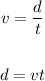
We know that time is constant, therefore we can establish the following:

`\begin{gathered} 3675=5\cdot(v_(plane)-v_(wind))\rightarrow3675=5v_(plane)-5v_(wind) \\ \\ 4275=5\cdot(v_(plane)+v_(wind))\rightarrow4275=5v_(plane)+5v_(wind) \end{gathered}`

We can solve the system by adding both equations, like this:

`\begin{gathered} 3675+4275=5v_(plane)-5v_(wind)+5v_(plane)+5v_(wind) \\ \\ 7950=10v_(plane) \\ \\ v_(plane)=(7950)/(10)=795\text{ km/h} \\ \\ \text{ To calculate the air rate it would be like this:} \\ \\ 4275=5v_(plane)+5v_(wind) \\ \\ 4275=5\cdot795+5v_(wind) \\ \\ 5v_(wind)=4275-3975 \\ \\ v_(wind)=(300)/(5)=60\text{ km/h} \\ \end{gathered}`

This means that the rate of the plane in still air is 795 km/h and the rate of the wind is 60 km/h