Question

the two triangles are similar. their areas and one side length are given. what is the ratio of the areas? what is the scale factor of the 2 sides? find the length of the corresponding side in the small triangle.

Answer 1

Let 'x' be the length of the corresponding side in the small triangle. Since both triangles are similar, we have the following equation:

`\begin{gathered} \frac{\text{area of big triangle}}{area\text{ of small triangle}}=((36)/(x))^2 \\ \Rightarrow(81)/(49)=(1296)/(x^2) \end{gathered}`

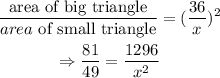
solving for 'x', we get:

`\begin{gathered} (81)/(49)=(1296)/(x^2) \\ \Rightarrow81\cdot x^2=1296\cdot49 \\ \Rightarrow81x^2=63504 \\ \Rightarrow x^2=(63504)/(81)=784 \\ \Rightarrow x=\sqrt[]{784}=28 \\ x=28 \end{gathered}`

therefore, the length of the corresponding side in the small triangle is 28 cm.

Now, we can find the ratio of the areas using the first equation. Let A be the area of the big triangle, and le t a be the area of the small triangle, then:

`\begin{gathered} (A)/(a)=((36)/(28))^2=1.65_{} \\ \Rightarrow A=1.65\cdot a \end{gathered}`

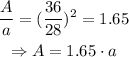
notice that the area of the big triangle is 1.65 times the area of the small triangle, thus, the ratio of the areas is:

`(81)/(49)=(1296)/(784)`

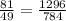
Finally, we have the following for the scale factor o the two corresponding sides:

`\begin{gathered} 28\cdot k=36 \\ \Rightarrow k=(36)/(28)=(9)/(7) \\ k=(9)/(7) \end{gathered}`

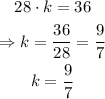
therefore, the scale factor of the two sides is k = 9/7