Question

Write a quadratic function with the roots at (3, 0) and (7, 0), and passing through the point (6, -9).

Answer 1

The equation is

`y=3x^2-30x+63`

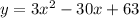
Step-by-step explanation:

Given:

The roots of the function is 3 and 7.

The function passes through the point (6,-9).

The objective is to find the quadratic function.

Consider the roots as,

`\begin{gathered} a=3 \\ b=7 \end{gathered}`

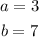
The quadratic function with the roots can be written as,

`y=k(x-a)(x-b)`

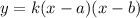
Substitute the values of roots in the above equation.

`y=k\lbrack(x-3)(x-7)\rbrack\text{..}...(1)`

The value of k can be calculated by substituting the point (x,y) = (6,-9) in the above equation.

`\begin{gathered} -9=k(6-3)(6-7) \\ -9=3k(-1) \\ -9=-3k \\ k=(-9)/(-3) \\ k=3 \end{gathered}`

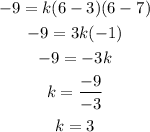
Now substitute the value of k in equation (1).

`\begin{gathered} y=3\lbrack(x-3)(x-7)\rbrack \\ =3\lbrack x^2-7x-3x+21\rbrack \\ =3\lbrack x^2-10x+21\rbrack \\ =3x^2-30x+63 \end{gathered}`

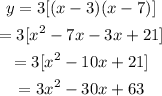
Hence, the required quadratic function is obtained.