We know the population distribution for the length of the rods: normal distribution with mean 105.2 cm and a standard deviation 1.7 cm.
In this case, we have a sample of 26 units, so we have to adjust the standard error to this sample size.
We have to calculate the probability that the sample mean is less than 104.3 cm.
We start by calculating the z-score for this sample mean value:
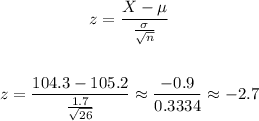
We can now calculate the probability by looking at the standard normal distribution:
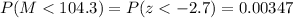
Answer: P(M < 104.3 cm) = 0.00347