Question

Question found in screenshot, it's only one question however, NOT 3.

Answer 1

Step 1

Given the function f defined in the question

Required: To find a relationship between a and b so that f is continuous at x=2

Step 2

`\lim _(x\rightarrow2^-)f(x)\text{ = }a(2)^2+b(2)`
`\lim _(x\rightarrow2^-)f(x)=4a+2b`
`\lim _{x\rightarrow2^{+^{}}}f(x)=5(2)-10=0`

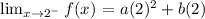
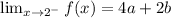
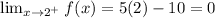
Step 3

For f to be continuous

`\lim _(x\rightarrow2^-)f(x)=\lim _(x\rightarrow2^+)f(x)_{}`

Hence,

`\begin{gathered} 4a+2b=0 \\ \text{Subtract 2b from both sides} \\ 4a+2b-2b=0-2b \\ \text{simplify} \\ 4a=-2b \\ or \\ -2b=4a \end{gathered}`
`\begin{gathered} \text{Divide through by -2} \\ (-2b)/(-2)=(4a)/(-2) \\ b=-2a \end{gathered}`

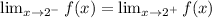
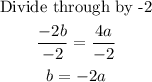
Hence, the relationship between a and b so that f(x) is continuous at x= 2 is seen below as;

b=-2a