Step 1
Given the function f defined in the question
Required: To find a relationship between a and b so that f is continuous at x=2
Step 2
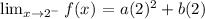
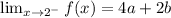
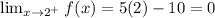
Step 3
For f to be continuous
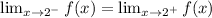
Hence,
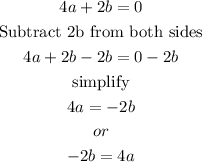
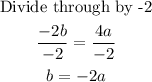
Hence, the relationship between a and b so that f(x) is continuous at x= 2 is seen below as;
b=-2a