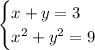
To solve the given system of equations:
1. Solve x in the first equation:
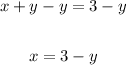
2. Use the value of x=3-y in the second equation:
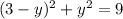
3. Solve y:
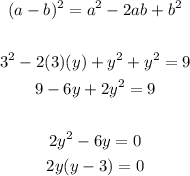
When the product of two factors is equal to zero, then you equal each factor to zero to find the solutions of the variable:
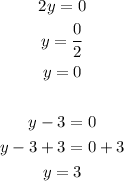
Then, the solutions for variable y in the given system are:
y=0
y=3
4. Use the values of y to find the corresponding values of x:
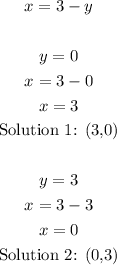
Then, the solutions for the given system of equations are: (3,0) and (0,3)quations
4. Use the values of y to find the corresponding values of x:
![undefined]()
4. Use the values of y to find the corresponding values of x:
![undefined]()