Question

How do I solve the trigonometric equation 2sin^2theta=1; for theta from 0 to 2pi

Answer 1

The question can be rewriten as:

`2\sin ^2(\theta)=1`

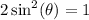
First, we isolate the sin(θ):

`\sin ^2\theta=(1)/(2)`

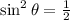
On the left side we have a value of [sin(Θ) ]². The first thing to do, so we isolate Θ, we must calculate the square root in both sides. It results in the following:

`\begin{gathered} \sqrt[]{\sin^2\theta}=\sqrt{(1)/(2)} \\ \sin \theta=\pm\sqrt[]{(1)/(2)}=\pm\frac{\sqrt[]{2}}{2} \end{gathered}`

If we apply the inverse function (sin⁻¹) in both sides, we can do as follow:

`\begin{gathered} \sin ^(-1)(\sin (\theta))=\sin ^(-1)(\pm\frac{\sqrt[]{2}}{2}) \\ \theta=\sin ^(-1)(\pm\frac{\sqrt[]{2}}{2}) \end{gathered}`

If we use ta unitary circle to better look at this, we can find two values of θ for each sine of θ. It is:

For the positive value of sin(θ), we find:

`\begin{gathered} \theta=45\degree=(\pi)/(4) \\ \theta=135\degree=(3\pi)/(4) \end{gathered}`

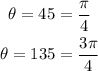
For the negative value of sin(θ), we find:

`\begin{gathered} \theta=225\degree=(5\pi)/(4) \\ \theta=315\degree=(7\pi)/(4) \end{gathered}`

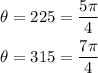
Because θ is from 0 to 2π, all this values satisfy the trigonometric equation. If you task is to find a single value for θ, you may use the fist one: π/4. Because it is more usual to work with sine with θ in the range of -π/2 to π/2, and the positive value is preferable.