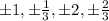Question

Be sure that no value in your list appears more than once.

Answer 1

Given the function:

`h(x)=-3x^3-2x^2-8x-2`

Let's use the rational zeros theorem to list all possible rational zeros of the given polynomial.

To use the rational roots theorem we have:

`\pm(p)/(q)`

Where p is a factor of the constaant (last term).

q is a factor of the leading coefficient,

Thus, we have:

p: Factors of -2 = ±1, ±2

q: Factors of -3 = ±1, ±3

The rational zero will be every combination of ±p/q.

Thus, we have:

`\begin{gathered} \pm(p)/(q)=\pm(1)/(1),\pm(1)/(3),\pm(2)/(1),\pm(2)/(3) \\ \end{gathered}`

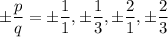
Simplify:

`\pm(p)/(q)=\pm1,\pm(1)/(3),\pm2,\pm(2)/(3)`

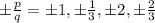
Therefore, the list of all possible rational zeros are:

`\pm1,\pm(1)/(3),\pm2,\pm(2)/(3)`

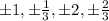
ANSWER:

`\pm1,\pm(1)/(3),\pm2,\pm(2)/(3)`