Question

the table shows the distance a person walks for exercise. find the rate of change in distance with respect to time.time(minutes) 30 60 90distance (miles) 1.5 3 4.5

Answer 1

We can start to answer this question taking into account that the rate of change is given by:

`\text{rateofchange=}\frac{change\text{ in y}}{\text{change in x}}=(y_2-y_1)/(x_2-x_1)_{}`

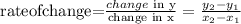
Then, we have from the table that we have three different values for y and three different values for x.

First, let us check that this rate of change is the same, that is if it is linear (it can be represented by a line) for these three different points:

x1 = 30

y1 = 1.5

x2 = 60

y2 = 3

Then, we have:

`r=(3-1.5)/(60-30)=(1.5)/(30)=0.05`

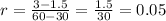
We have that the rate of change is 0.05 miles per minute.

Let us check the second rate of change:

x1 = 60

y1 = 3

x2 = 90

y2 = 4.5

Then, we have that the rate of change is:

`r=(4.5-3)/(90-60)=(1.5)/(30)=0.05`

We got the same rate of change of 0.05 miles per minute in both cases. Therefore, the rate of change in distance with respect to time is 0.05 miles per minute.