Answer:
Given that, to find the rule of the reflection.
Step-by-step explanation:
Let us consider, the scale of the given graph be 1 unit.
To find the rule, first to find the axis of reflection.
Point A is (-4,0)
Point B is (-3,-1)
Point C is (-5,-4)
The image points are,
Point A' is (0,-4)
Point B' is (-1,-3)
PointC' is (-4,-5)
From the relection rule we have that
each point on the figure is translated an equal distance across the line of symmetry, back on to the figure.
If the given figure reflects over a line y=x, the points of preimage and points of image is of the form,
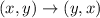
the points of the original image is transformed to points of the image as follows the above transformation, then the Reflection is over the line y=x.
The required rule of reflection is,
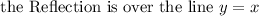
Answer is: Reflection is over the line y=x.