Question

A sample of nitrogen gas has a volume of 10L at 101.3 kPa and 20 °C. To preserve biological tissue, the nitrogen gas is cooled to -190 °C, almost the temperature of liquid nitrogen, at a pressure of 101.3 kPa. What volume will thenitorgen occupy at this temperature?

Answer 1

Let's assuming the gas will behave as an Ideal Gas.

We have two states:

State 1:

- Temperature: 20°C

- Pressure: 101.3 kPa

- Volume: 10L

State 2:

- Temperature: -190°C

- Pressure: 101.3 kPa

- Volume: ?

We can see that the pressure is the same, so we can look only at the relation between Temperature and Volume. One law that works with constant pressure is the Charles' Law, and it says that, for an ideal gas, a change with constant pressure will have the absolute temperature and the volume as direct proportional, that is:

`(V)/(T)=k`

Where k is a constant.

So, in state 1, we have:

`(V_1)/(T_1)=k`

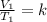
And in state 2 we have:

`(V_2)/(T_2)=k`

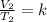
Since the "k" is the same, we can say that:

`(V_1)/(T_1)=(V_2)/(T_2)`

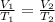
However, the temperature must be in absolute term, that is, we need to convert it to Kelvin.

This can be done by adding 273.15 to the temperature in degress Celsius:

`\begin{gathered} T_1=20\degree C=(20+273.15)K=293.15K \\ T_2=-190\degree C=(-190+273.15)K=83.15K \end{gathered}`

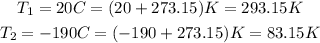
Now, we can just substitute the values and solve for V2:

`\begin{gathered} V_1=10L \\ T_1=293.15K_{} \\ T_2=83.15K \\ (V_1)/(T_1)=(V_2)/(T_2)_{} \\ (10L)/(293.15K)=(V_2)/(83.15K) \\ (10L)/(293.15K)\cdot83.15K=V_2 \\ V_2=\frac{10L}{293.15\cancel{K}}\cdot83.15\cancel{K} \\ V_2=2.8364\ldots L\approx2.8L \end{gathered}`

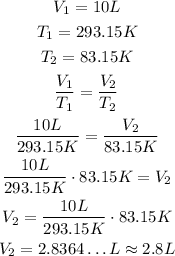
So, the nitrogen will occupy approximately 2.8L.