Step 1. The expression that we have is:
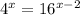
To prove that we get the same answer if we use a logarithm base 2 and a logarithm base 4, we will solve the equation using both and check that the result is the same.
Step 2. To solve using a base 2 logarithm, we apply it to both sides of the equation:
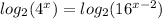
Using the following property of logarithms:
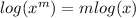
The expression is simplified as follows:
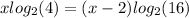
The base 2 logarithm of 4 and 16 is:
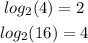
Substituting these values into the equation:
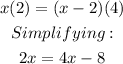
Solving for x:
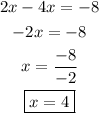
Step 3. Now we repeat the process but this time we use the logarithm base 4.
The expression is:
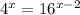
Applying logarithm base 4 to both sides:
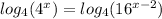
Simplifying:
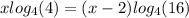
The base 4 logarithm of 4 and 16 is:
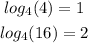
Substituting these values into our equation:
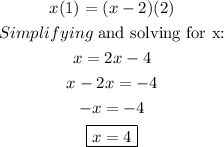
Answer: We have proven that we get the same result using a base 2 logarithm and a base 4 logarithm.