Polar coordinates are generally written as :
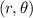
And the rectangular coordinate equivalent (x,y) is obtained using the following relationships:
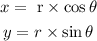
Now, since the given polar coordinate is:
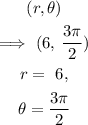
Therefore, the corresponding rectangular coordinate is :
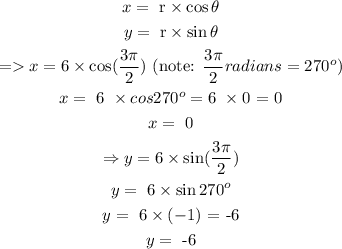
Therefore, the rectangular coordinate equivalent (x,y) is (0,-6)