Question

based on a survey of random samples from Saint Joseph citizens the proportion of citizens interested in creating a Riverfront tourist area is 71 with a margin of error of .04 what interval contains the margin of error of 95% of the sample proportions?

Answer 1

In order to find the interval for 95% of the sample proportions, we need to find the z-scores for the interval of 95% in the normal distribution.

To do so, we can find the z value for 2.5% and 97.5% (this way, we can subtract then and find the interval of 95%).

Looking at the table, we have that z1 = -1.96 for 0.025 and z2 = 1.96 for 0.975.

Now, finding the interval, we have that:

`\begin{gathered} \text{interval}=\lbrack\mu+\sigma\cdot z1,\mu+\sigma\cdot z2\rbrack \\ \text{interval}=\lbrack71+0.04\cdot(-1.96),71+0.04\cdot1.96\rbrack \\ \text{interval}=\lbrack71-0.0784,71+0.0784\rbrack \\ \text{interval}=\lbrack70.9216,71.0784\rbrack \end{gathered}`

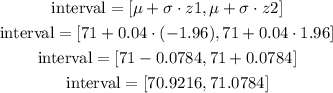
So the interval is from 70.9216 to 71.0784.