a) Amount left = 45000 - 780h
b) 45000 - 780h > 15000
c) No, it won't
Step-by-step explanation:
a) The water is drained at rate = 780 gallons per hour
Initial gallons of water = 45000
let the number of hours = h
Amount remaining after h hours:
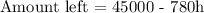
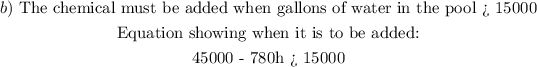

Hence for the chemical to be added, it will take less than 38.46 hours
2 days in hours = 2(24) = 48 hours
48 hours > 38.46 hours
As a result, it would take less than two days before the chemical is added.
No, It won't