SOLUTION
Step1: write out the expression
![\sqrt[]{125x}](https://img.qammunity.org/2023/formulas/mathematics/college/icfwf70i7zrz2bodryskley67yf69gj26r.png)
we have to write this expression in its simplest form to identify the value of A and B
Step2: Identify the perfect square and write has a product
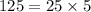
Step3: replace the product above with 125 in the expression
![\sqrt[]{125x}=\sqrt[]{25*5* x}](https://img.qammunity.org/2023/formulas/mathematics/college/ut6kgei0tlff5p5ypf5zq2sz7cnelkzcvm.png)
Step4: simplify the last expression by applying the rational rule below
![\sqrt[]{a* b}=\sqrt[]{a}*\sqrt[]{b}](https://img.qammunity.org/2023/formulas/mathematics/college/knj5e2lzb1tn4a002eyi5qadgnrkm4nfvk.png)
Hence we have
![\sqrt[]{25*5* x}=\sqrt[]{25}*\sqrt[]{5}*\sqrt[]{x}](https://img.qammunity.org/2023/formulas/mathematics/college/93kzbe3jya50jxjdu8effkgono1m86346q.png)
![\sqrt[]{25}*\sqrt[]{5}*\sqrt[]{x}=5*\sqrt[]{5}*\sqrt[]{x}=5\sqrt[]{5x}](https://img.qammunity.org/2023/formulas/mathematics/college/xn2ssbic4khpm5nfic81hwq7u5t4saqqui.png)
Hence
![\sqrt[]{125x}=5\sqrt[]{5x}](https://img.qammunity.org/2023/formulas/mathematics/college/ixpey5xc7b31ojon3nnf2vn91raelq11ce.png)
Therefore
A=5 and B=5x