Given:
The length of the triangle is: 27, 3, x, y, and z.
Find: Value of "y"
Sol:
In triangle ACD is:
Use Pythagoras theorem:
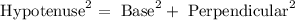
Apply for triangle ACD then:
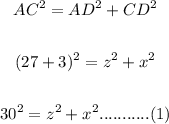
In triangle CBD
Apply theorem then:
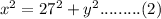
In Triangle ABD
Apply theorem then:
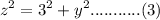
From eq (2) and eq(3) put the value in eq(1) then:
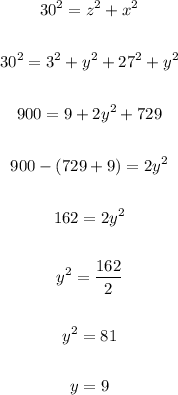
So the value of "y" is 9.