Question

Hi, can you help me answer this question, please, thank you!

Answer 1

In this question we have 4 items. Let's answer each one of them individually.

item (a):

To answer this question, first we need to convert our desired value into a z-score. For all of the items, we have the following mean(mu) and standard deviation(sigma):

`\begin{cases}\mu=42.3 \\ \sigma=13.8\end{cases}`

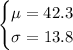
The formula to convert a value from our distribution to a z-score is:

`z=(x-\mu)/(\sigma)`

With x = 57.5, we have the following z-score:

`z=(57.5-42.3)/(13.8)\approx1.10`

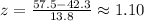
Using a z-table(right), we can find the area to the right hand side of the curve. Those values represent the area between z = 0 and any positive value, we just need to find the area between z = 0 to our z-score.

According to this z-table, the area between 42.3 gallons and 57.5 gallons is 36.43% of the whole area. Since the normal distribution is symmetric, from the mean 42.3 gallons to the left we have 50% of the graph. Then, the probability of having the consumption below 57.5 is the sum of those two values.

`0.5+0.3643=0.8643`

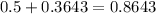
Then, this is our answer.

`P(x<57.5)=0.8643`

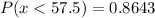
item (b):