Question

Help with homework please .Part 2. Find the mass of the pyramid in grams.

Answer 1

Given:

• Side length of base = 18.2 centimeters

,

• Height of pyramid = 23.1 centimeters

,

• Mass of pyramid = 2.75 kilograms

Let's find the volume of the pyramid.

To find the volume of the pyramid, apply the formula:

`V=a^2*(h)/(3)`

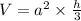
Where:

a is the side length of the base = 18.2 cm

h is the height = 23.1 cm

Input values into the formula and solve for the volume, V.

`\begin{gathered} V=18.2^2*(23.1)/(3) \\ \\ V=331.24*7.7 \\ \\ V=2550.55cm^3 \end{gathered}`

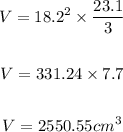
Therefore, the small solid pyramid has a volume of approximately 2550.55 cubic centimeters.

• Part 2.

Find the mass of the pyramid in grams.

Given the mass = 2.75 kilograms

To find the mass in grams, apply the standard unit of measurement.

Where:

1 kilogram = 1000 grams

Thus, we have:

`2.75kg=2.75*1000=2750\text{ grams}`

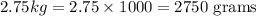
Therefore, the mass in grams is 2750 grams.

• Part 3.

Let's find the density of the pyramid in grams per cubic centimeter.

To find the density, apply the formula:

`density=\frac{mass}{\text{volume}}`

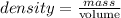
Thus, we have:

`\begin{gathered} density=\frac{2750\text{ }}{2550.55} \\ \\ \text{density}=1.08\text{ g/}cm^3 \end{gathered}`

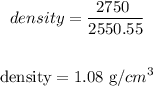
Therefore, the density is 1.08 grams per cubic centimeter.

ANSWER:

Part 1: 2550.55 cubic centimeters

Part 2: 2750 grams

Part 3: 1.08 grams per cubic centimeter.