Question

Which values from the set (-6. -4, -3, -1, 0, 2) satisfy this inequality? -1/2x+3≥50 -4 -3. -1, 0, and 2 only O-1, 0 and 2 only 0-6, -4, -3, and -1 only 0 -6 and -4 only

Answer 1

D, -6 and -4 only​

Step-by-step explanation:

Given the inequality:

`-(1)/(2)x+3\ge5`

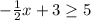
First, subtract 3 from both sides:

`\begin{gathered} -(1)/(2)x+3-3\ge5-3 \\ -(1)/(2)x\ge2 \end{gathered}`

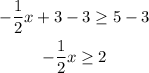
Next, multiply both sides by -2.

`\begin{gathered} -(1)/(2)x*-2\le2*-2 \\ x\le-4 \end{gathered}`

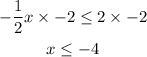
Note that when inequality is multiplied by a negative number, the inequality sign is reversed.

Therefore, the values from the set (-6. -4, -3, -1, 0, 2) that satisfy this inequality are: -6 and -4 only​