Question

Identify whether the given points are collinear by completing the average rate of change between all input-output pairs

Answer 1

Step-by-step explanation:

When two or more points are collinear, it means they lie on the same line

Thus, if they are on the same line, the average rate of change is expected to be the same

Between two points, we have the average rate of change calculated as:

`\Delta\text{ = }(y_2-y_1)/(x_2-x_1)`

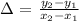
Let us have the points labelled A,B and C

Between A and B, we have the average rate of change as:

`\Delta\text{ = }(2\pi+1-\pi)/(4-0)\text{ = }(\pi+1)/(4)`

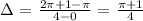
Between A and C, we have the average rate of change as:

`\Delta\text{ = }(3\pi+2-\pi)/(6-0)\text{ = }(2\pi+2)/(6)\text{ = }(\pi+1)/(3)`

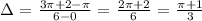
Between B and C, we have the average rate of change as:

`\Delta\text{ = }(3\pi+2-(2\pi+1))/(6-4)\text{ = }(\pi+1)/(2)`

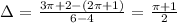
We can see that the rate of change is not the same and it is safe to say that the points are not collinear