Question

A sphere is inscribed in a right circular cylinder, such that it is tangent to both bases. What is the ratio of the volume of the sphere to the volume of the cylinder?

Answer 1

We are given that a sphere is inscribed is a right circular cylinder. This means that the diameter of the sphere is equivalent to the height of the cylinder. A front view of this is the following:

We notice that the radius of the sphere and the radius of the cylinder coincide.

Now, we are asked to determine the ratio of the volume of the sphere to the volume of the cylinder. First, the volume of a sphere is given by:

`V_S=(4)/(3)\pi r^3_{}`

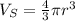
And the volume of a cylinder is given by:

`V_c=\pi r^2h`

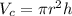
Now, the ratio is the quotient between the volumes, therefore, we have:

`(V_s)/(V_c)=\frac{(4)/(3)\pi r^3_{}}{\pi r^2h}`

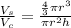
We can cancel out pi:

`(V_s)/(V_c)=\frac{(4)/(3)r^3_{}}{r^2h}`

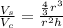
We can also cancel out the square of the radius:

`(V_s)/(V_c)=\frac{(4)/(3)r^{}_{}}{h}`

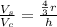
Now, We know that the height "h" of the cylinder is equivalent to the diameter, this means that the height if equivalent to two times the radius, that is:

`h=2r`

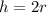
Substituting in the ratio we get:

`(V_s)/(V_c)=\frac{(4)/(3)r^{}_{}}{2r}`

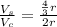
Now we cancel out the radius:

`(V_s)/(V_c)=((4)/(3))/(2)`

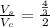
Simplifying the fraction we get:

`(V_s)/(V_c)=(4)/(6)`

Therefore, the ratio is 4/6.