Question

Hello, can you please help me solve question 3 !!

Answer 1

`\cos (2t)-2\sin ^2(t)=0`

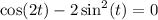
Use the next trigonometric rules:

`\begin{gathered} \cos 2t=\cos ^2t-\sin ^2t \\ \\ \sin ^2t=1-\cos ^2t \end{gathered}`

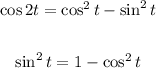
Use Cos2t

`\cos ^2t-\sin ^2t-2\sin ^2t=0`

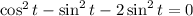
Combine similar terms:

`\cos ^2t-3\sin ^2t=0`

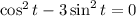
Use sin²t:

`\begin{gathered} \cos ^2t-3(1-\cos ^2t)=0 \\ \\ \cos ^2t-3+3\cos ^2t=0 \end{gathered}`

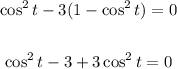
Combine similar terms:

`4\cos ^2t-3=0`

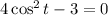
Add 3 in both sides of the equation:

`\begin{gathered} 4\cos ^2t-3+3=0+3 \\ 4\cos ^2t=3 \end{gathered}`

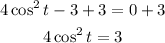
Divide both sides of the equation into 4:

`\begin{gathered} (4\cos ^2t)/(4)=(3)/(4) \\ \\ \cos ^2t=(3)/(4) \end{gathered}`

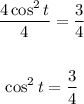
Find the square root of both sides of the equation:

`\begin{gathered} \sqrt[]{\cos^2t}=\sqrt[]{(3)/(4)} \\ \\ \cos t=\pm\frac{\sqrt[]{3}}{2} \\ \\ \cos t=+\frac{\sqrt[]{3}}{2} \\ \\ \cos t=-\frac{\sqrt[]{3}}{2} \end{gathered}`

Use the unit circle to find wich angles in the given interval have a cos equal to:

`\cos t=\pm\frac{\sqrt[]{3}}{2}`

Solution:

`t=(\pi)/(6),(5\pi)/(6),(7\pi)/(6),(11\pi)/(6)`