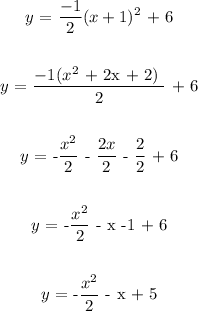Question

The quadratic function has a maximum value of g(-1)=6 and goes through g(-3)=4. Write the quadratic equation in standard form.

Answer 1

The quadratic equation is;

`\begin{gathered} y\text{ = -}(x^2)/(2)\text{ - x + 5} \\ \\ \text{where a = -}(1)/(2)\text{ , b = -1 and c = 5} \end{gathered}`

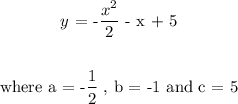
Here, given the information in the question, we want to write the quadratic equation in its standard form

To do this we shall make some substitutions;

The maximum point of the quadratic equation is also called the vertex

In this question, the vertex is g(-1) = 6

So this is (-1,6)

The other point is g(-3) = 4

So the point here is (-3,4)

Thus, we have a quadratic equation with vertex (-1,6) that passes through the point (-3,4)

The general equation for a quadratic equation having a vertex and passing through a given point is;

`y=a(x-h)^2\text{ + k}`

where (h,k) represents the coordinates of the vertex and (x,y) represents the coordinates of the points that the quadratic equation passes through

Thus, we have;

`y=a(x+1)^2\text{ + 6}`

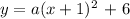
so to get the a value in this form, we substitute the values of the points; where x is -3 and y is 4

We have;

`\begin{gathered} 4=a(-3+1)^2\text{ + 6} \\ \\ 4\text{ = 4a + 6} \\ 4a\text{ = 4-6} \\ 4a\text{ = -2} \\ \\ a\text{ = }(-2)/(4) \\ \\ a\text{ = }(-1)/(2) \end{gathered}`

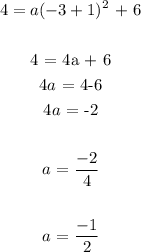
So the quadratic equation can be written as;

`y\text{ = }(-1)/(2)(x+1)^2\text{ + 6}`

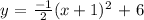
We can rewrite this in the form in the question as follows;

`\begin{gathered} y\text{ = }(-1)/(2)(x+1)^2\text{ + 6} \\ \\ y\text{ = }\frac{-1(x^2\text{ + 2x + 2) }}{2}\text{ + 6} \\ \\ y\text{ = -}(x^2)/(2)\text{ - }(2x)/(2)\text{ - }(2)/(2)\text{ + 6} \\ \\ y\text{ = -}(x^2)/(2)\text{ - x -1 + 6} \\ \\ y\text{ = -}(x^2)/(2)\text{ - x + 5} \end{gathered}`