Sample standard deviation:
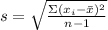
To find the standard deviation of the given set:
1. Fidn the mean:
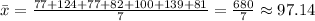
2. Find the (x-mean) for each data:
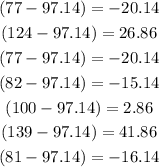
3. Square the results you get in previous step:
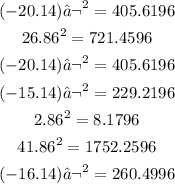
4. Add the squares you get in previus step:

5. Divide the resull above into n-1:
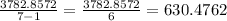
6. Find the square root of the quotient you get in previous step:
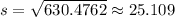
Then, the standard deviation is 25.109