Okay, here we have this:
Considering the provided function, we are going to calculate the asymptotes, so we obtain the following:
Vertical asymptotes:
They correspond to the singularities of the functions or zeros of the denominator, in this case:
2x+1=0
2x=-1
x=-1/2
The vertical asymptote is x=-1/2.
Horizontal asymptotes:
Since the degree of the numerator is equal to the degree of the denominator plus 1, the asymptote is steep, and corresponds to the quotient of the polynomial division. Then:
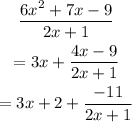
Therefore the sloped asymptote is:
y=3x+2
Graphing the function and asymptotes: