Question

Suppose Elsa borrows $6500 at an interest rate of 8% compounded each year.Assume that no payments are made on the loan.Follow the instructions below. Do not do any rounding.

Answer 1

(a) At the end of one year, the amount is $7020

(b) At the end of 2 years, the amount is $7581.6

Step-by-step explanation:

To solve this problem, we need to use the compound interest formula:

`A=P(1+r)^t`

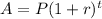
Where:

• P is the initial amount

,

• r is the rate of annual compounding in decimal

,

• t is the time in years

,

• A is the amount after t years

In this case,

P = $6500

r = 0.08 (to convert 8% to decimal, we divide by 100. 8/100 = 0.08)

To solve (a), t = 1 (one year of compounding):

`\begin{gathered} A=6500(1+0.08)^1 \\ A=6500\cdot1.08 \\ A=7020 \end{gathered}`

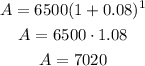
After 1 year, the amount is %7020

To solve (b), t = 2:

`\begin{gathered} A=6500(1+0.08)^2 \\ A=6500\cdot1.1664 \\ A=7581.6 \end{gathered}`

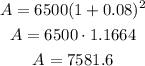
After 2 years, the amount is $7581.6