We have this two functions:
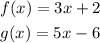
We have to calculate what f/g is.
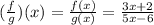
What is the domain of (f/g)(x)?
The domain is all the values of x for which the function has a defined value.
That means that if the denominator becames 0, the function is not defined.
This happens when 5x-6=0:
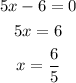
Then, the domain is "all the real numbers different from 5/6".