Question

Identify a Ferris wheel with a radius of 9.5 m that rotates fully once every 10 seconds on a numeric model (minimum 5 data points).

Answer 1

Given:

The radius of the Ferries wheel is 9.5m.

The number of second the ferries wheel take to rotate fully =10 seconds.

Aim:

We need to find the numeric model for the given situation.

Step-by-step explanation:

The full rotation is 360 degrees.

The wheel rotates 360 degrees per 10 seconds.

Divide 360 by 10, we get

`(360)/(10)=36^{o\text{ }}\text{ per second.}`

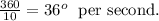
The wheel rotates 36 degrees per second.

Take that we traveled t seconds.

The point on the circle is y.

The angle is 36t degrees.

The height from the ground is 9.5+h.

The radius is 9.5m.

Consider the triangle that makes an angle of 36 t degrees,

Adjacent side = 9.5-h m and hypotenuse is 9.5 m.

Consider the cosine formula.

`\cos \theta=\frac{\text{Adjacent side}}{\text{Hypotenuse}}`

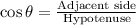
Substitute adjacent side = 9.5-h m and the hypotenuse is 9.5 m.

`\cos 36t^o=(9.5-h)/(9.5)`

`\cos 36t^o=(9.5-h)/(9.5)`

`9.5\cos 36t^o=9.5-h`

`h=9.5-9.5\cos 36t^o`

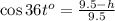
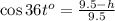
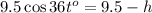
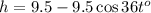
The graph of the function is