Question

How much money will there be in an account at the end of 9 years if $15000 is deposited at 7% interest compounded quarterly? (Assume no withdrawals are made.)

Answer 1

In order to calculate the amount on an account that has a certain compounded interest, we need to use the following expression:

`A=P\cdot(1+(r)/(n))^(nt)`

Where "A" is the final amount, "P" is the principal invested on the account, "r" is the annual interest rate, "n" is the number of times the amount is compounded in a year and "t" is the elapsed time in years.

On this case P is equal to 15000, r is equal to 0.07, n is equal to 4 (because it gets compounded four times in a year). With this we can find A.

`\begin{gathered} A=15000\cdot(1+(0.07)/(4))^(4\cdot9) \\ A=15000\cdot(1+0.0175)^(36) \\ A=15000\cdot(1.0175)^(36) \\ A=15000\cdot1.8674 \\ A=28011.11 \end{gathered}`

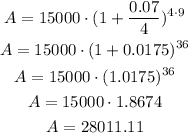
The amount at the end of the 9 years will be 28011.11