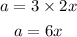Answer:
a=6x
Step-by-step explanation:
Given the logarithmic equation:
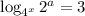
We appy the change of base rule:
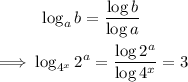
Next, rewrite 4 as a power of 2.

Take the index of the numbers as the product by the index law.
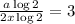
Cancel out log 2 in the numerator and denominator
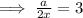
Finally, cross multiply to express "a" in terms of x.