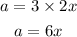Question

Please read and follow the instructions to the practice problem in the picture, I need help, I’m having trouble with this * This is calculus *

Answer 1

a=6x

Step-by-step explanation:

Given the logarithmic equation:

`\log _(4^x)2^a=3`

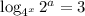
We appy the change of base rule:

`\begin{gathered} \log _ab=(\log b)/(\log a) \\ \implies\log _(4^x)2^a=(\log2^a)/(\log4^x)=3 \end{gathered}`

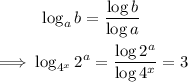
Next, rewrite 4 as a power of 2.

`\begin{gathered} (\log2^a)/(\log4^x)=3 \\ \implies(\log 2^a)/(\log 2^(2x))=3 \end{gathered}`

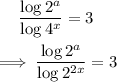
Take the index of the numbers as the product by the index law.

`(a\log 2)/(2x\log 2)=3`

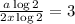
Cancel out log 2 in the numerator and denominator

`\implies(a)/(2x)=3`

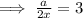
Finally, cross multiply to express "a" in terms of x.

`\begin{gathered} a=3*2x \\ a=6x \end{gathered}`