Question

Which of the following is another way to describe the vector 5i - 12j? magnitude 13 and S67°W magnitude 13 and S23°W magnitude 13 and S67°E magnitude 13 and S23°E

Answer 1

Magnitude 13 and S23°E

Explanation:

Given the vector:

`5i-12j`

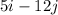
We want to find its (a)magnitude (b)direction.

Given a vector ai+bj, its magnitude and direction are calculated using the formulas:

`\begin{gathered} Magnitude:r=√(a^2+b^2) \\ Direction:\theta=\tan^(-1)((b)/(a)) \end{gathered}`

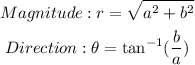
Therefore, for the given vector:

`\begin{gathered} r=√(5^2+(-12)^2)=√(25+144)=√(169)=13 \\ \theta=\tan^(-1)(-(12)/(5))=-67.4\degree\approx-67\degree \end{gathered}`

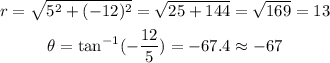
However, from the diagram of the vector below:

Since the angle is in Quadrant IV:

`-67.4\degree=360-67=293\degree=S23\degree E`

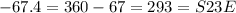
The magnitude of the vector is 13, and its direction is S23°E.

The last option is correct.