A)
Let:
u1 = Initial speed of ball A = 4.6
v1 = Initial speed of ball B = 0
u2 = Final speed of ball A = 2.4
v2 = Final speed of ball B = u
m1 = m2 = Mass of ball A
So:
Using the conservation of momentum:
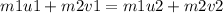
Since the masses are the same:

Expressing the speeds in a rectangular forms:

So:
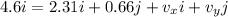
So:
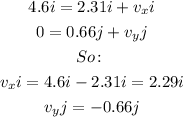
Now, we can calculate the angle as follows:
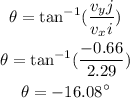
B) The speed is given by:
![\begin{gathered} u=\sqrt[]{v_xi^2+v_yj^2} \\ u=\sqrt[]{2.29^2+(-0.66)^2} \\ u=2.38(m)/(s) \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/y4jvcilpuuc9rkf75ntwym45nu1ueoq07m.png)