Question

Eric plotted the graph below to show the relationship between the temperature of his city and the number of cups of lemonade he sold daily Lemonade Sales Cups of lemonade Part A: Describe the relationship between the temperature of the city and the number of cups of lemonade sold. Part B: Describe how you can make the line of best fit. Write the approximate slope and y-intercept of the line of best fit. Show your work use to calculate the slope and y-intercept.

Answer 1

Part A

People will buy more lemonades as the city got hotter.

There is a positive correlation between Cups of lemonade sold and the the temperature in the city.

The higher the temperature, the more cups of lemonade will be required.

Part B

Approximate equation of the straight line

y = 0.2x

Slope = 0.2

y-intercept = 0

Step-by-step explanation

Part A

Like you have rightly determined, there is a positive correlation between Cups of lemonade sold and the the temperature in the city.

The higher the temperature, the more cups of lemonade will be sold.

So, it is true that people will buy more lemonades as the city got hotter.

Part B

To do this part, we would need to truly fit in a line amongst all of the points marked out such that the number of points on either sides of line is almost the same. That is why it is called the line of best fit, as this line is the line that best fits into the points plotted.

After the line is obtained, we can now work out the slope and the y-intercept from what we know about straight lines.

This next part about fitting the line in between the points really depends on each person, but the results of each person shouldn't vary too much.

So, the line I fit into these points passed through the points (40, 8) and (60, 12).

So, with these two points we can write the equation of the line.

The general form of the equation in point-slope form is

y - y₁ = m (x - x₁)

where

y = y-coordinate of a point on the line.

y₁ = This refers to the y-coordinate of a given point on the line

m = slope of the line.

x = x-coordinate of the point on the line whose y-coordinate is y.

x₁ = x-coordinate of the given point on the line

So we just need to calculate the slope and use one of the points to calculate the equation of the line.

For a straight line, the slope of the line can be obtained when the coordinates of two points on the line are known. If the coordinates are (x₁, y₁) and (x₂, y₂), the slope is given as

`Slope=m=\frac{Change\text{ in y}}{Change\text{ in x}}=(y_2-y_1)/(x_2-x_1)`

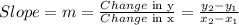
For this question,

(x₁, y₁) and (x₂, y₂) are (40, 8) and (60, 12)

`\text{Slope = }(12-8)/(60-40)=(4)/(20)=0.2`

Recall that

y - y₁ = m (x - x₁)

m = slope = 0.2

Point = (x₁, y₁) = (40, 8)

x₁ = 40

y₁ = 8

y - y₁ = m (x - x₁)

y - 8 = 0.2 (x - 40)

y - 8 = 0.2x - 8

y = 0.2x - 8 + 8

y = 0.2x

for the y-intercept, when x = 0

y = 0.2x

y = 0.2(0)

y = 0

So,

y-intercept = 0

Hope this Helps!!!