SOLUTION:
Step 1:
In this question, we are given the following:
A foam cylinder, with a diameter of 3 inches and a height of 8 inches, is carved into the shape of a cone.
What is the maximum volume of a cone that can be carved? Round your answer to the hundredth place.
Step 2:
The details of the solution are as follows:
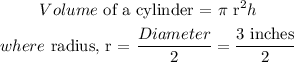
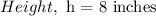
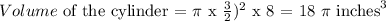
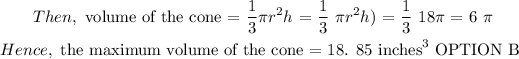
CONCLUSION:
The