Question

A man running at a speed of 12m/s grabs a rope and swings upward. What is the maximum height he could reach?

Answer 1

Draw a diagram to visualize the situation:

The man will travel up using the rope until all of its initial kinetic energy is converted into gravitational potential energy.

At the beginning of the swing, the man's potential energy is 0 and its kinetic energy is:

`K=(1)/(2)mv^2`

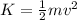
At the end of the swing, his kinetic energy is 0 and its potential energy is:

`U=mgh`

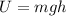
Where h is the maximum height.

Since all the kinetic energy is converted into potential energy, then:

`\begin{gathered} U=K \\ \Rightarrow mgh=(1)/(2)mv^2 \end{gathered}`

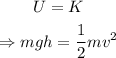
Isolate h from the equation:

`h=(v^2)/(2g)`

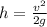
Replace v=12m/s and g=9.81m/s^2 to find the maximum height he can reach:

`h=((12(m)/(s))^2)/(2(9.81(m)/(s^2)))=7.34m`

Therefore, the maximum height that the man can reach is approximately 7.34m.