Answer:
y=-(2/5)x+2
Explanation:
Given the equation of the line:
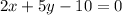
The slope-intercept form of a line is given as y=mx+b.
Thus, make y the subject of the given equation.
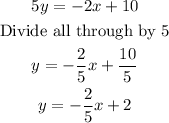
The slope-intercept form of the equation is y=-(2/5)x+2.
Next, the lines are graphed using the intercepts.
When y=0
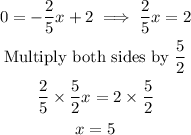
• The x-intercept is (5,0)
,
• From the slope-intercept form, the y-intercept is (0,2).
Join the two points using a straight line as shown below: