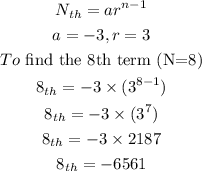The sequence of numbers is an arithmetic sequence. The sequence,
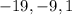
has a common difference of 10.
This is derived by deducting each term from the next one. That is deduct the first term from the second term, deduct the second term from the third, and so on. So you would have,
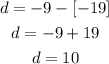
To find the nth term, we shall apply the formula;
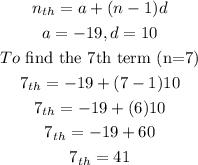
The 7th term in the sequence is 41
For the sequence,
-3, -9, -27...
What we have is a geometric sequence and the common ratio is derived by dividing each term by the next one. So you would have
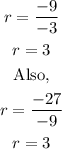
To find the nth term of a geometric sequence;