Answer:
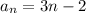
Step-by-step explanation:
The formula for the nth term of an arithmetic sequence is
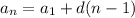
Where:
a_n is the term we want to find
a_1 is the first term of the sequence
d is the common distance between the terms.
In this sequence, we can see that d = 3. Because any term minus the previous is 3:
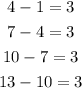
The first term is 1. Then:

Now, we can apply distributive property:
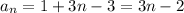
And we get the final expression for the arithmetic sequence formula for the nth term:
