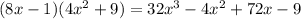Given the expressions:

You can multiply the binomials of the first expression in order to expand it. You can use the FOIL Method to multiply them, which states that:
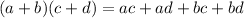
You also need to remember the Sign Rules for Multiplication:

Then:
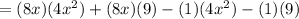
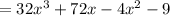
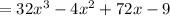
By definition, Equivalent Expressions work the same, but they have different forms.
Since:
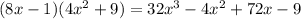
You can conclude that they are Equivalent Expressions.
Hence, the answer is: They are Equivalent Expression, because: