Question

A medical equipment industry manufactures X-ray machines. The unit cost C (the cost in dollars to make each X-ray machine) depends on the number of machines made. If x machines are made, then the unit cost is given by the function C(x) = 0.2.x2 - 100x +31,146. What is the minimum unit cost? Do not round your answer.

Answer 1

We have the unit cost function C(x) expressed as:

`C(x)=0.2x^2-100x+31146`

We can find the minimum unit cost by deriving C(x) and equal the result to 0. Then, we can clear the value of x:

`\begin{gathered} (dC)/(dx)=0.2\cdot2x-100\cdot1+31146\cdot0 \\ (dC)/(dx)=0.4x-100 \end{gathered}`
`\begin{gathered} (dC)/(dx)=0 \\ 0.4x-100=0 \\ 0.4x=100 \\ x=(100)/(0.4) \\ x=250 \end{gathered}`

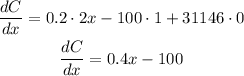
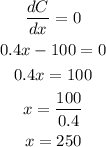
Now, we can calculate the minimum cost by calculating C(250):

`\begin{gathered} C(250)=0.2\cdot(250)^2-100\cdot250+31146 \\ C(250)=0.2\cdot62500-25000+31146 \\ C(250)=12500-25000+31146 \\ C(250)=18646 \end{gathered}`

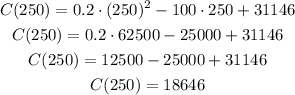
Answer: the minimum unit cost is $18,646