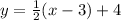ANSWER:
The center is:
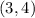
Vertex with larger y-value:
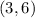
Vertex with smaller y-value:

Foci with larger y-value:
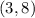
Foci with smaller y-value:
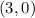
Equation of an asymptote:

Where
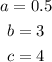
Step-by-step explanation:
We have to take this equation into the general form of an hyperbola:
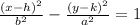
Where (h,k) is the center of the hyperbola.
We also know the vertices are:
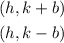
The foci are:
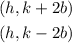
And that the asymptotes are given by the expression:

Let's manipulate the equation:
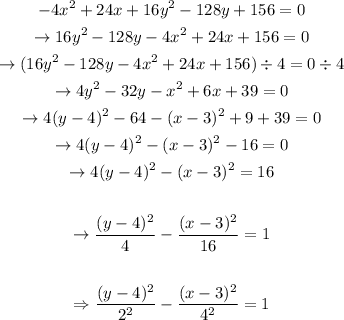
From this general equation, we can conclude that the center is:
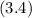
Now, the vertices are:
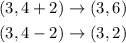
The foci are:
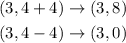
And the equation of the asympotes are:
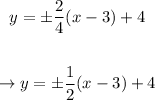
One of this asymptotes is: