Complete the equation for the piece wise function graphed below.

Question

asked Jun 19, 2023 159k views

1 Answer

JNevill · Answer 1 · 2023-06-24T14:17:48+0000

Answer:

$f(x)=\mleft\{\begin{aligned}-0.5x+3,if-6\le x\le-2 \\ -3,if-2Explanation:For the value of x such that: -6≤x≤-2We have the endpoints (-6,0) and (-2, -2).We determine the equation in the slope-intercept form, y=mx+b.[tex]\begin{gathered} \text{Slope,m}=(0-(-2))/(-6-(-2)) \\ =(2)/(-6+2) \\ =(2)/(-4) \\ m=-0.5 \end{gathered}$

The equation then becomes:

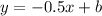
Using the point (-6,0)

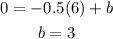
$\begin{gathered} 0=-0.5(6)+b \\ b=3 \end{gathered}$

Therefore: f(x)=-0.5x+3, -6≤x≤-2

Next, f(x)=-3 for -2

Finally, for 1The endpoints are (1,-4) and (6,1)

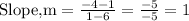
$\text{Slope,m}=(-4-1)/(1-6)=(-5)/(-5)=1$

Using the point (1,-4)

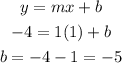
$\begin{gathered} y=mx+b \\ -4=1(1)+b \\ b=-4-1=-5 \end{gathered}$

Therefore, f(x)=x-5, for 1

The completed function will now be:

[tex]f(x)=\mleft\{\begin{aligned}-0.5x+3,-6\le x\le-2 \\ -3,-2

Complete the equation for the piece wise function graphed below.

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

Please log in or register to add a comment.

No related questions found

Categories

Other Questions