Question

A vector points -43.0 unitsalong the X-axis, and 11.1 unitsalong the y-axis.Find the magnitude of thevector.

Answer 1

The magnitude of the vector is 44.4 units

To find the magnitude of a vector that points along the X-axis and Y-axis, we can use the Pythagorean theorem, which is applicable to right-angled triangles. The magnitude of a vector
`\(\vec{V}\) with components \(V_x\) and \(V_y\)` along the X and Y axes, respectively, is given by the formula:

`\[ |\vec{V}| = √(V_x^2 + V_y^2) \]`

Where:

-
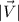`\( |\vec{V}| \)` is the magnitude of the vector.

-
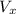`\( V_x \)` is the component of the vector along the X-axis.

-
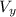`\( V_y \)`is the component of the vector along the Y-axis.

Given:

-
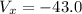`\( V_x = -43.0 \)` units (the negative sign indicates the direction is opposite to the positive X-axis direction)

-
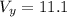`\( V_y = 11.1 \)` units

Now, we will substitute these values into the formula to calculate the magnitude of the vector:

`\[ |\vec{V}| = √((-43.0)^2 + (11.1)^2) \]`

Let's calculate this value.

The magnitude of the vector that points -43.0 units along the X-axis and 11.1 units along the Y-axis is approximately 44.4 units.

Answer 2

Answer:

The magnitude of the vectior = 44.38 units

Direction of the vector, θ = -14.47

Explanations:

The vector points -43.0 units along the X-axis, and 11.1 units along the y-axis.

This can be graphically illustrated as shown below:

x = -43

y = 11.1

The magnitude, R, is calculated using the Pythagora's theorem

`\begin{gathered} R^2=x^2+y^2 \\ R^2=(-43)^2+(11)^2 \\ R^2\text{ = }1849+121 \\ R^2\text{ = }1970 \\ R\text{ = }\sqrt[]{1970} \\ R\text{ = }44.38 \end{gathered}`

The magnitude of the vectior = 44.38 units

The direction of the vector is calculated below:

`\begin{gathered} \tan ^{}\theta\text{ = }\frac{\text{Opposite}}{\text{Adjacent}} \\ \tan \theta\text{ = }(11.1)/(-43) \\ \tan \theta\text{ = -}0.258 \\ \theta\text{ = }\tan ^(-1)(-0.258) \\ \theta\text{ = }-14.47^0 \end{gathered}`