Question

Hello! I need some assistance with this homework question, pleaseQ10

Answer 1

We can do the following steps to find the quotient difference for the given function.

Step 1: We find f(x + h). For this, we replace x = x + h into the given function.

`\begin{gathered} f(x)=\sqrt[]{x-16} \\ f(x+h)=\sqrt[]{x+h-16} \end{gathered}`

Step 2: We apply the quotient difference formula.

`(f(x+h)-f(x))/(h)=\frac{\sqrt[]{x+h-16}-\sqrt[]{x-16}}{h}`

Step 3: We rationalize the numerator. For this, we multiply by the conjugate of the numerator.

`\begin{gathered} \text{ Multiply by }\sqrt[]{x+h-16}+\sqrt[]{x-16}\text{ on the numerator and the denominator} \\ (f(x+h)-f(x))/(h)=\frac{\sqrt[]{x+h-16}-\sqrt[]{x-16}}{h}\cdot\frac{\sqrt[]{x+h-16}+\sqrt[]{x-16}\text{ }}{\sqrt[]{x+h-16}+\sqrt[]{x-16}\text{ }} \\ (f(x+h)-f(x))/(h)=\frac{(\sqrt[]{x+h-16}-\sqrt[]{x-16})(\sqrt[]{x+h-16}+\sqrt[]{x-16}\text{ })}{h(\sqrt[]{x+h-16}+\sqrt[]{x-16}\text{ })} \end{gathered}`

Step 4: We simplify as much as we can. For this, we factor the numerator using the difference of squares formula.

`(a+b)(a-b)=a^2-b^2\Rightarrow\text{ Difference of squares }`

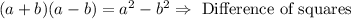
Then, we have:

`\begin{gathered} a=\sqrt[]{x+h-16} \\ b=\sqrt[]{x-16} \\ (f(x+h)-f(x))/(h)=\frac{(\sqrt[]{x+h-16})^2-(\sqrt[]{x-16})^2}{h(\sqrt[]{x+h-16}+\sqrt[]{x-16}\text{ })} \\ (f(x+h)-f(x))/(h)=\frac{x+h-16-(x-16)^{}}{h(\sqrt[]{x+h-16}+\sqrt[]{x-16}\text{ })} \\ (f(x+h)-f(x))/(h)=\frac{x+h-16-x+16^{}}{h(\sqrt[]{x+h-16}+\sqrt[]{x-16}\text{ })} \\ (f(x+h)-f(x))/(h)=\frac{h^{}}{h(\sqrt[]{x+h-16}+\sqrt[]{x-16}\text{ })} \\ (f(x+h)-f(x))/(h)=\frac{1^{}}{\sqrt[]{x+h-16}+\sqrt[]{x-16}} \end{gathered}`

Therefore, the difference quotient of the function is:

`\frac{1^{}}{\sqrt[]{x+h-16}+\sqrt[]{x-16}}`