Given:
The speed of the wave is,
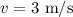
The distance between adjacent crests is,
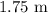
To find:
a) What is the frequency of the waves?
b) What is the period of the waves?
Step-by-step explanation:
a) The horizontal distance between two adjacent crests or troughs is known as the wavelength.
The wavelength is,
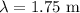
The frequency is,
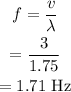
Hence, the frequency is 1.71 Hz.
b)
The period of waves is,
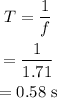
Hence, the period of waves is 0.58 s.