Question

What is the absolute difference between the sum of the multiples of two from 1 and 100, inclusive, and the sum of the multiples of three from 1 and 100, inclusive?

Answer 1

The absolute difference between the sum of the multiples of two from 1 and 100, inclusive, and the sum of the multiples of three from 1 and 100, inclusive = 867

Step-by-step explanation

To solve this, we need to first find the sum of multiples of 2 from 1 to 100 inclusive and find the sum of multiples of 3 from 1 to 100 inclusive. These set of numbers, form an arithmetic progression because all the terms have the same common difference

To do that, we need to note that the sum of an arithmetic progression is given as

`\text{Sum = }(n)/(2)\lbrack2a+(n-1)d\rbrack`

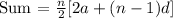
a = First term

n = number of terms

d = common difference

For the multiples of 2

a = 2

n = 50

d = 2

`\begin{gathered} \text{Sum = }(n)/(2)\lbrack2a+(n-1)d\rbrack \\ \text{Sum = }(50)/(2)\lbrack2(2)+(49-1)(2)\rbrack \\ =(50)/(2)\lbrack4+(48*2)\rbrack \\ =(50)/(2)\lbrack4+96\rbrack \\ =(50)/(2)(102) \\ =2550 \end{gathered}`

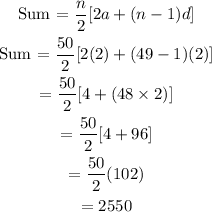
For the multiples of 3

a = 3

n = 33

d = 3

`\begin{gathered} \text{Sum = }(n)/(2)\lbrack2a+(n-1)d\rbrack \\ \text{Sum }=(33)/(2)\lbrack2(3)+(33-1)(3)\rbrack \\ =(33)/(2)\lbrack6+(32*3)\rbrack \\ =(33)/(2)\lbrack6+96\rbrack \\ =(33)/(2)(102) \\ =1683 \end{gathered}`

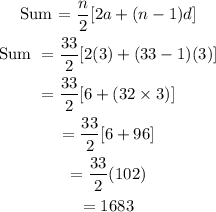
So,

The absolute difference = |(Sum of multiples of two from 1 to 100 incusive) - (Sum of multiples of three from 1 to 100 incusive)

= |2550 - 1683|

= 867

Hope this Helps!!!