ANSWER
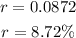
Step-by-step explanation
We want to find the rate at which the amount was continuously compounded.
The formula for the total amount for a continuously compounded principal is:
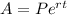
where A = amount
P = principal
r = rate
t = time (in years)
Substituting the given values into the equation:
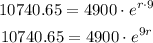
Divide both sides by 4900:
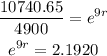
Find the natural logarithm of both sides of the equation:
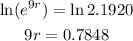
Divide both sides by 9:
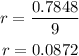
Convert to decimal number:
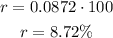
That is the interest rate.